MATEMATIKA

V.ROVNICE  A NEROVNICE

Rovnice – rovnost dvou výrazů

Ekvivalentní úprava rovnice – úprava, při které se nemění množina řešení rovnice

1. přičtení libovolného čísle k oběma stranám rovnice
2. násobení obou stran rovnice libovolným nenulovým číslem nebo výrazem
3. dělení obou stran rovnice libovolným nenulovým číslem nebo výrazem
4. výměna stran rovnice
5. nahrazení libovolné strany rovnice číslem, který se jí rovná
6. umocnění obou stran rovnice na druhou, nabývají-li obě strany rovnice v celém definičním oboru nezáporných hodnot
7. odmocnění obou stran rovnice na druhou, nabývají-li obě strany rovnice v celém definičním oboru nezáporných hodnot

Dovolené ( neekvivalentní úpravy ) rovnic – musíme provést zkoušku, protože řešení takto upravené rovnice nemusí být řešením původní rovnice

1. Umocnění obou stran rovnice
2. Násobení obou stran rovnice výrazem definovaným v definičním oboru rovnice

Nerovnice – nerovnost dvou výrazů

Lineární nerovnice upravujeme stejným způsobem jako rovnice. Kvadratické nerovnice převedeme do součinového tvaru, nerovnice s neznámou ve jmenovateli ( nerovnice v podílovém tvaru) řešíme pomocí nulových bodů.

Výjimka :  Násobíme- li nerovnici záporným číslem, musíme změnit znaménko nerovnosti na opačné

Před řešení rovnice i nerovnice musíme určit definiční obor rovnice a po jejím vyřešení provést srovnání výsledku s definičním oborem !!!!!!!!!!!!!!

Typy rovnic:

1. Lineární rovnice -     a x + b = 0 , a,b є R

Způsob řešení : 1. Odstraníme zlomky

                      2. Odstraníme závorky

                      3.  Převedeme na tvar a x = b

                     4. Vyjádříme x = b/a

2. Kvadratické rovnice -    a x² + b x + c = 0     a,b,c є R , a ≠ 0

Způsob řešení : 1. Ekvivalentními úpravami převedeme na daný tvar

                              2. Určíme diskriminant     D = b² – 4 a c

                                         D = 0  →  rovnice má v R 1 řešení

                                         D < 0  →  rovnice nemá  řešení v R

                                         D > 0  →  rovnice má v R 2 řešení

                               3. Určíme množinu řešení pomocí vzorce

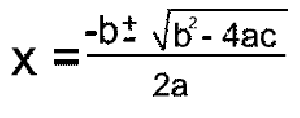
Typy kvadratických rovnic  :   a = 1  →  rovnice je v normovaném tvaru

                                                  b nebo c = 0 → neúplná kvadratická rovnice

Viettovy vzorce – platí pro rovnici v normovaném tvaru   x² + p x + q = 0

                                       x_{1 .}  x₂  = q

                              x_{1 +} x₂  = -p

 Každou kvadratickou rovnici lze napsat ve tvaru  

                   a . ( x - x₁) . ( x - x₂) = 0

3. Logaritmické a exponenciální rovnice – rovnice , ve kterých se vyskytuje neznámá v exponentu, nebo logaritmu

Způsob řešení : 1. zp. Převedení na společný základ nebo exponent

                              2. zp. Substituce

Při úpravách používáme vzorce pro počítání s mocninami a logaritmy

log_a x = y   právě tehdy když a^y =x

log_a x + log_a y = log_a x . y 

log_a x - log_a y  = log_a x : y 

log_a x ⁿ = n . log_a x

a^r   .   a^s   =   a^r+s

a^r   :   a^s   =   a^r-s

(a^r )^s  =  a^r.s

(a.b)^r  =  a^r.b^r

(a:b)^r  =  a^r:b^r

a^-n  = 1/aⁿ

POZOR! Definiční obor logaritmické rovnice – logaritmované číslo musí být větší než 0

 3. Iracionální rovnice – rovnice s neznámou pod odmocninou

Způsob řešení -  odmocninu osamostatníme na jednu stranu a rovnici umocníme. Pokud se vyskytuje v rovnici dvě a více odmocnin, provedeme tento krok několikrát, tak abychom odmocniny odstranili.

POZOR! Tato úprava je pouze dovolená. Musíme provést zkoušku!!!!!!!!!!!!

POZOR! Pod sudou odmocninou může být pouze kladné číslo nebo nula.

4. Soustavy rovnic o několika neznámých – převedeme na jednu rovnici o jedné neznámé

Způsoby řešení : 1. Dosazovací metoda

                                2. Sčítací metoda

                                3. Grafická metoda

                                4. Matice

5. Rovnice s absolutní hodnotou – rovnice v nichž se neznámá vyskytuje v absolutní hodnotě

Způsob řešení : 1. Určíme nulové body

                              2. Rozdělíme definiční obor na jednotlivé intervaly podle nulových bodů

                              3. Provádíme diskusi pro jednotlivé intervaly